# JS的浮点运算精度问题
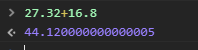
如上图所示,在JS中浮点数的运算会出现精度问题,更简单的有:
0.1 + 0.2 = 0.30000000000000004。究其原因,我们是以十进制输入的数字,但是计算机是以二进制运行的。程序中计算两个十进制的数,计算机需要将其转换为二进制,运算结束后再转为十进制返回,转换是不完美的。。
虽然JS中一般不涉及比较复杂的浮点数运算,但也不是绝对的用不到,还是要处理一下的。
# 一、简单的处理
如果业务中的数字不那么敏感,这个敏感的意思是指对数字的精度要求不高,而不是涉及支付、金融等。。
// + - * /
(num1 + num2).toFixed(2)// 保留两位小数
1
2
2
🤐简单的处理。。。
# 二、精度较高的处理
JS中小数运算会产生问题,但是整数运算并不会如此,可以将小数运算转换为整数运算。
首先需要获取一个浮点数的小数部分长度。
# 获取小数部分长度
// 获取小数部分长度
function getDecimalLength (num) {
let len = 0;
try {
let _num = Number(num);// 可以转换使用科学计数法的数字
let strArr = (_num + '').split('.');
if (strArr.length === 2) {
len = parseInt(strArr[1]) === 0 ? 0 : strArr[1].length;
} else {
len = 0;
}
} catch (e) {
throw e;
}
return len;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# 具体实现
// +
function add (num1, num2) {
let dl1 = getDecimalLength(num1),// num1小数长度
dl2 = getDecimalLength(num2),// num2小数长度
n;// 倍数
n = Math.pow(10, Math.max(dl1, dl2));// 小数部分长度需用最长的那一个
return Math.round(Number(num1) * n + Number(num2) * n) / n;
}
// -
function subtract (num1, num2) {
let dl1 = getDecimalLength(num1),
dl2 = getDecimalLength(num2),
n;
n = Math.pow(10, Math.max(dl1, dl2));
return Math.round(Number(num1) * n - Number(num2) * n) / n;
}
// *
function multiply (num1, num2) {
let dl1 = getDecimalLength(num1),
dl2 = getDecimalLength(num2),
n;
n = Math.pow(10, Math.max(dl1, dl2));
return (Number(num1) * n) * (Number(num2) * n) / (n * n);
}
// /
function divide (num1, num2) {
let dl1 = getDecimalLength(num1),
dl2 = getDecimalLength(num2),
n;
n = Math.pow(10, Math.max(dl1, dl2));
return (Number(num1) * n) / (Number(num2) * n);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
# 测试
add(0.1, 0.2);// 0.3
subtract(0.56, 0.19);// 0.37 -> 0.56 - 0.19 = 0.37000000000000005
multiply(0.142, 0.2);// 0.0284 -> 0.142 * 0.2 = 0.028399999999999998
divide(0.211111, 0.1);// 2.11111 -> 0.211111 / 0.1 = 2.1111099999999996
add(1e-1,2e-1);// 0.3
1
2
3
4
5
2
3
4
5